Pranto Shohan

Emergence

Computational Growth of Urban Organism

"The ecological neighbourhood is a living system, one that is never static. It displays the same evolutionary characters as living organisms and thus evolves over time".

RESILIENCE AND EVOLUTION

Neighbourhood Design Guidelines

Overview

What distinguishes the organic growth of a city from its planned development?

My undergraduate final year thesis explores the concept that cities function as living organisms, with interdependent layers of systems that can be designed computationally. Living in Dhaka, one of the fastest-growing cities in the world, I witnessed firsthand the pressing need for sustainable urban development. Over the past 30 years, Dhaka's rapid expansion has severely impacted its ecology, environment and livability. Addressing these challenges requires a novel approach to urban planning that considers Dhaka's unique landform and ecology. I employed computational simulation methods to mimic natural systems, optimizing various urban layers such as landform, connectivity, and zoning.

Context

Dhaka’s urban expansion vs. wetland geography and ecologicaly.

Dhaka is one of the most densely populated cities in the world, experiencing rapid growth over the past 30 years alongside a steady decline in its wetlands and natural landscapes. Despite its distinct geographical characteristics, the predominant growth strategy has been to landfill wetlands and impose a rigid grid-like road pattern. However, the outskirts of Dhaka reveal a contrasting narrative—a more organic and adaptive form of settlement growth.

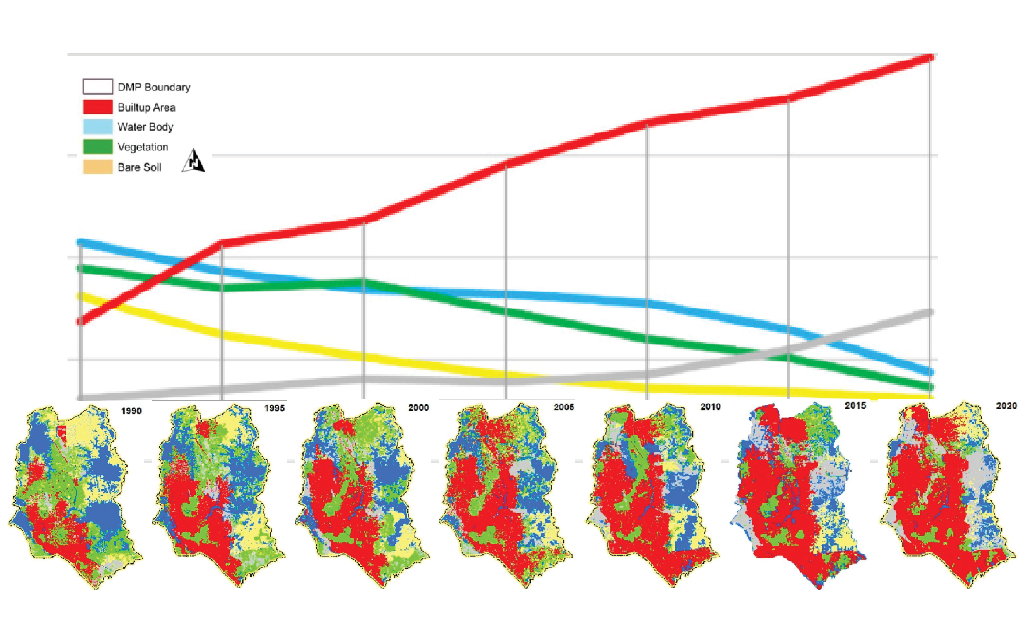
Land use and land cover change map of Dhaka for the years 1990, 1995, 2000, 2005, 2010, 2015, and 2020.

Rahman, Md & Szabó, György. (2021)

land cover change 1990-2020.

Google Earth

Site

Uttara Phase-3 is one of the three largest housing projects undertaken by RAJUK, Dhaka's planning body, but the extent of wetland destruction it has caused is alarming.

Uttara Phase-3 Before and After: 2004-2023

Google Earth

Urban Organism

Like organisms, cities function through interdependent systems.

Cities and organisms share many similarities in terms of circulation, resource cycles, information networks, and the positioning of their components. While organisms have evolved to develop highly efficient and intelligent designs, cities have grown through the collective intelligence of people. By mimicking organic systems in the planning process, we can find more effective solutions through computational methods.

Landform System

Dhaka has a unique landscape. The Madhupur Tract in greater Dhaka is surrounded by rivers that flood every year, bringing fresh water inland. Over thousands of years, these floods have shaped the land into amoeboid patterns. The highlands are bordered by lower-lying areas that are used for agriculture during the dry season. Water has seeped into every nook and cranny of the land, creating a distinctive geography.

Natural Landform of Madhupur Tract

Google Earth

This is Reaction-Diffusion and it occurs in many other places in nature, both organic and inorganic.

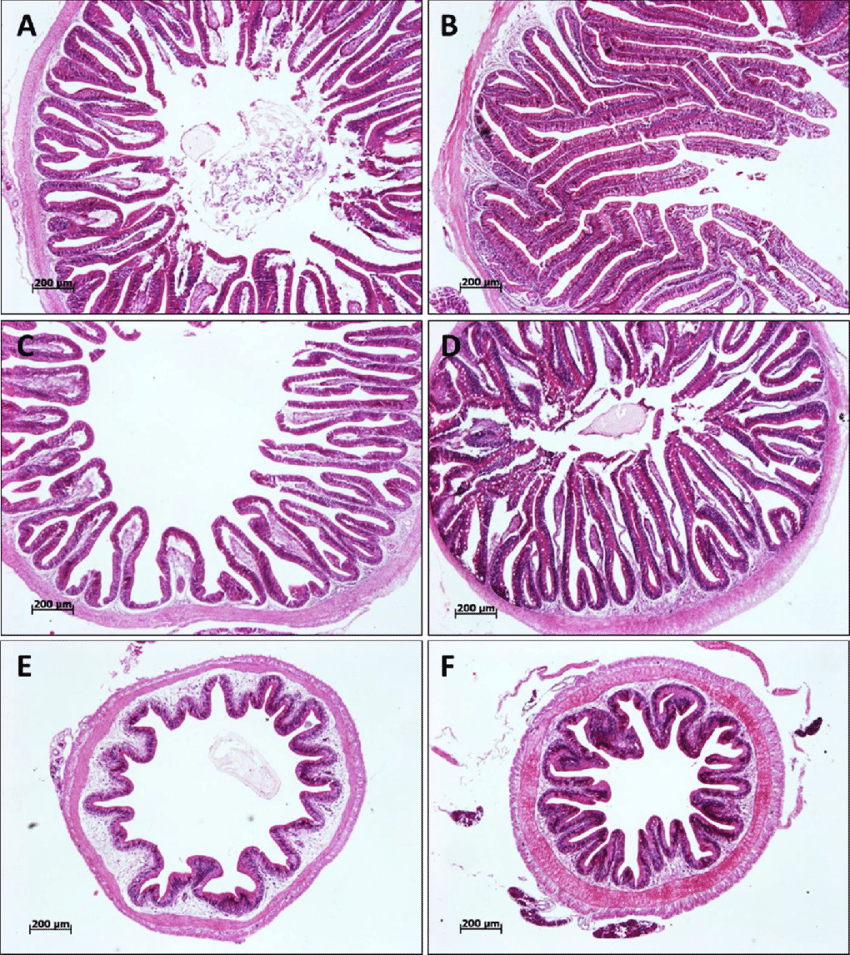
Fish Intestine and Effects of Magnetic and Electric Fields

Boonanuntanasarn, Surintorn & Khaomek, Pranorm & Pitaksong, Taratip & Hua, Yanling. (2014).

Differential growth or reaction diffusion can be simulated with an algorithm and it can give us a pattern similar to the landform of Dhaka.

Algorithmic representation of differential growth

python


import ghpythonlib.components as gh
import Rhino.Geometry as R


#if "IdCount" not in globals() or Reset:
#    IdCount = 0




class Point:
    idCount = 0
    def __init__(self, p):
        self.id = Point.idCount
        self.geo = p
        self.Force = R.Vector3d(0, 0, 0)
        self.TotalCollision = 0
        Point.idCount += 1

    def __str__(self):
        return "Circle:" + str(self.id)

    def applyForce(self, force):
        self.Force += force
        self.TotalCollision += 1
        
    def collide(self, other, Radius):
        distance = self.geo.DistanceTo(other.geo)
        if (distance < Radius):
            #print(distance, Radius)
            direction = R.Vector3d(self.geo - other.geo)
            direction.Unitize()
            move = direction * 0.5 * (Radius - distance)
            self.applyForce((move))
            other.applyForce(-move)
            print(str(self) + " collides with " + str(other) + " Force: "+ str(self.Force) + " Distance: " + str(distance))
            
    def bound(self):
        for b in Boundary:
            dis = R.Curve.ClosestPoint(b, self.geo, Radius)
            if(dis[0]):
                Result = gh.CurveClosestPoint(self.geo, b)
                point = Result[0]
                direction = R.Vector3d(self.geo - point)
                direction.Unitize()
                move = direction * 0.005 * Result[1]
                self.applyForce((move))
    #            self.collide(dis[1], Radius)
    def move(self):
        temp = self.Force / self.TotalCollision
        self.geo += temp
        print("Moved with force: " + str(temp))
        self.Force = R.Vector3d(0,0,0)
        self.TotalCollision = 1

class Island:
    def __init__(self, pointList):
        self.points = []
        for p in pointList:
            self.points.append(Point(p))

    def grow(self):
        for i in range(len(self.points)):
            if(i < len(self.points)-1):
                dis = self.points[i].geo.DistanceTo(self.points[i+1].geo)
                if (dis > Radius):
                    ngeo = (self.points[i].geo + self.points[i+1].geo)/2
                    new = Point(ngeo)
                    self.points.insert(i+1, new)
                    PointList.append(new)


# Instantiate or reset persistent variable
if "T" not in globals() or Reset:
    T = 0

if "Islands" not in globals() or Reset:
    Islands = []
    for curve in IslandCurves:
        points = gh.DivideDistance(curve, 60)[0]
        Islands.append(Island(points))

if "PointList" not in globals() or Reset:
    PointList = []
    for i in Islands:
        for p in i.points:
            PointList.append(p)







def main():
    for point in PointList:
        for other in PointList:
            if point != other:
                print("Attempting to collide:", T)
                point.collide(other, Radius)

    for point in PointList:
        point.bound()
    for point in PointList:
        point.move()

    for i in Islands:
        i.grow()
#    
#    PointList = []
#    for i in Islands:
#        for p in i.points:
#            PointList.append(p)





# Update the variable and component
if T < Iterations:
    T = T + 1
    main()


I = []
for i in Islands:
    points = []
    for p in i.points:
        points.append(p.geo)
    
    crv = gh.PolyLine(points, True)
    I.append(crv)

#
#r = []
#for p in PointList:
#    r.append(p.geo)

Time = T
Relaxed = I

Relating the natural geography with the differential growth, we can use this model to design landform that will maintain the flow of water during flooding season. This pattern also maximizes the lenght of edge ecology.

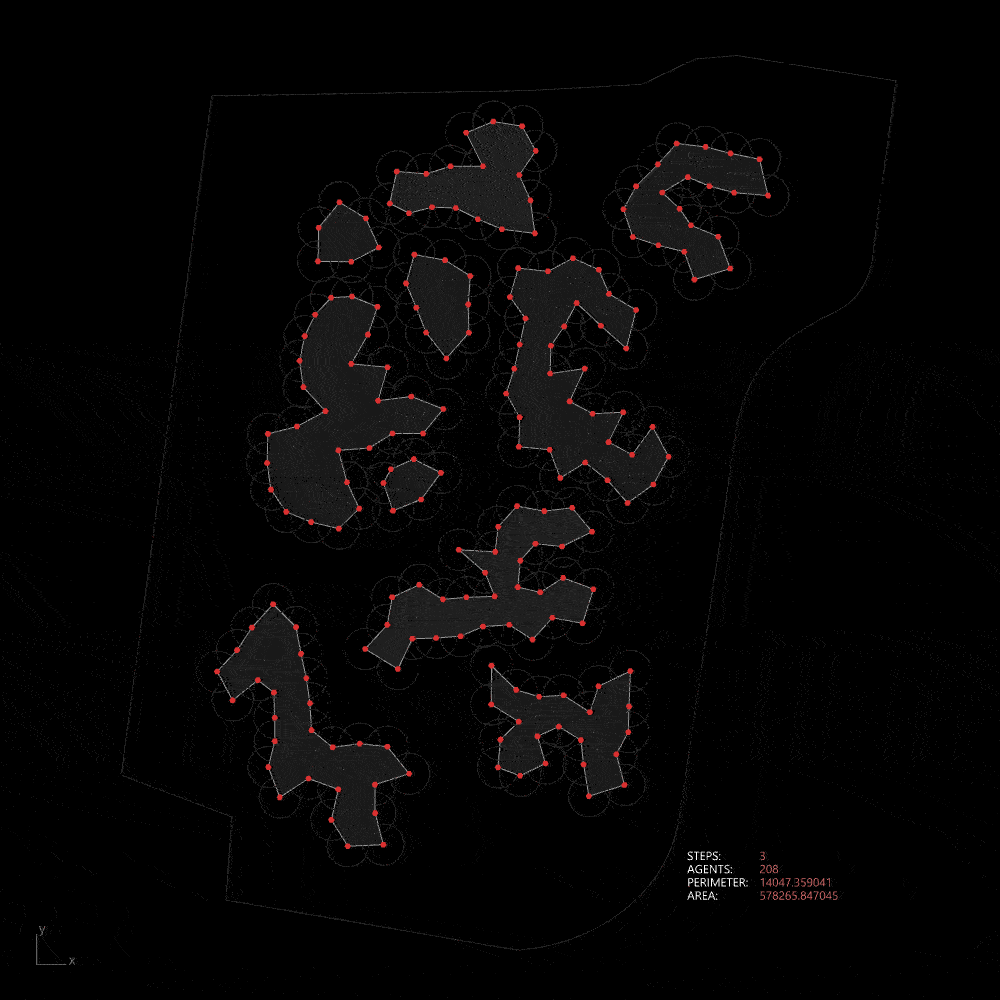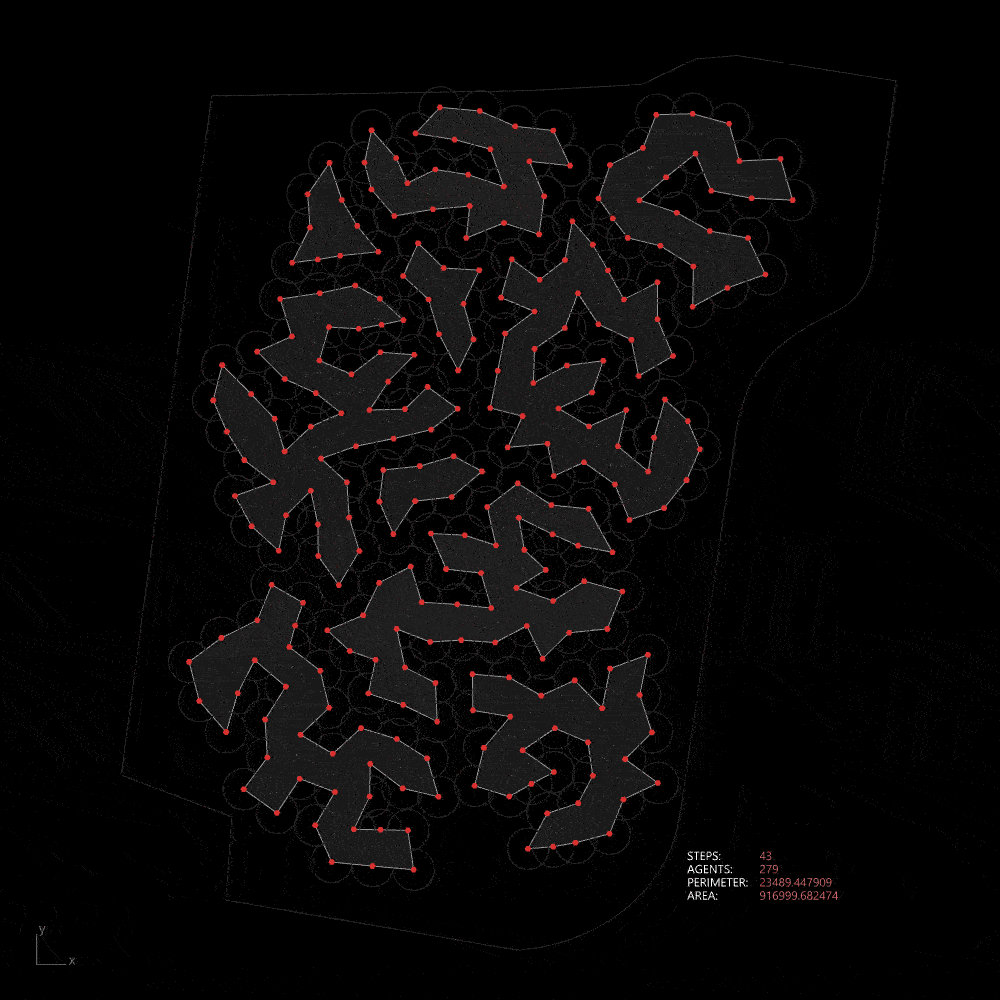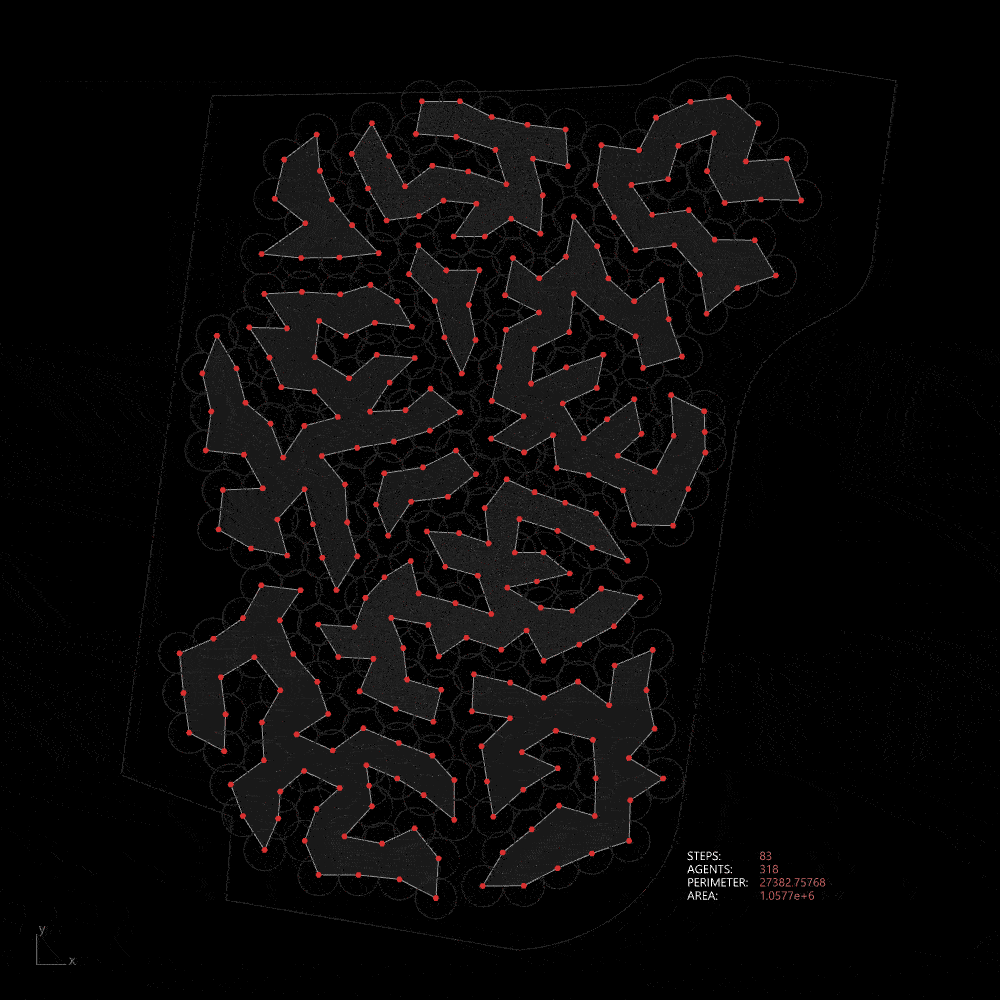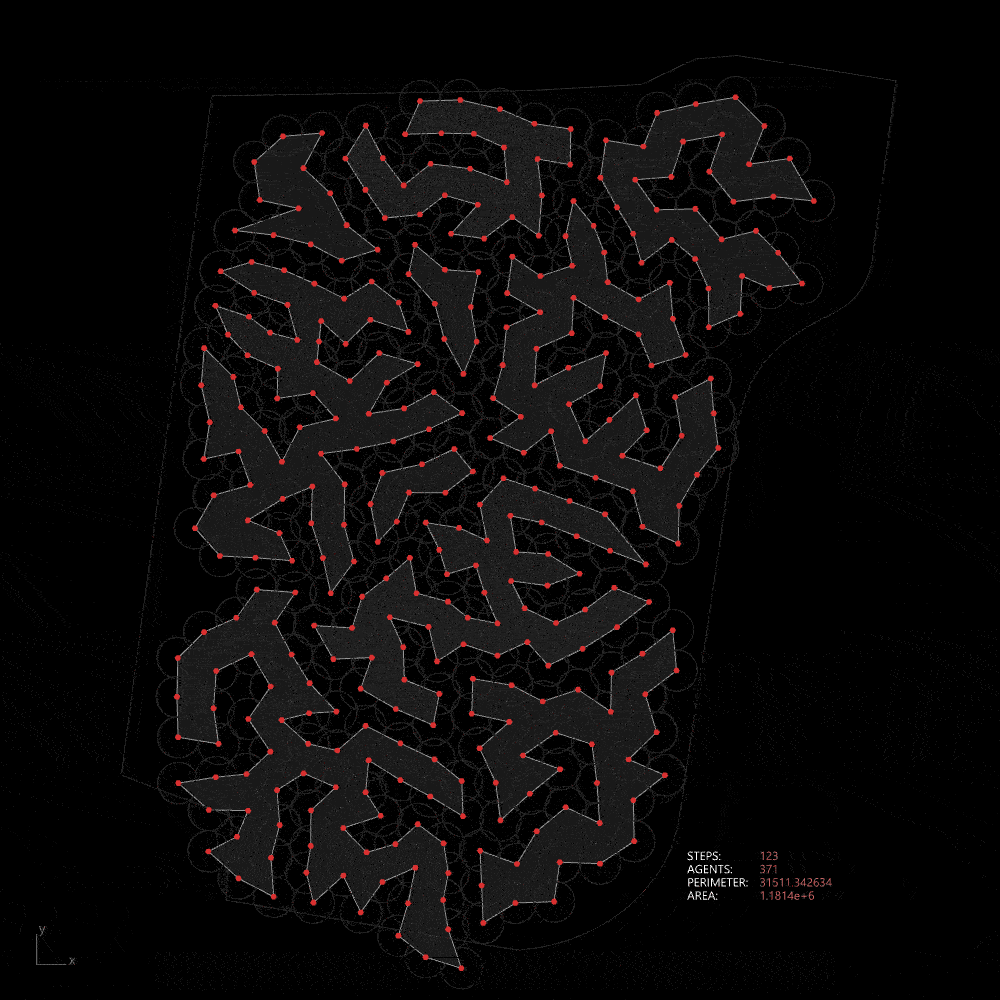
Differential growth in the site

Connectivity System

This basic connectivity problem is not new in nature. almost every organism deals with the transportation problem in some way. Slime molds can optimize connectivity among the food sources. Ants can collectively create more efficient routes. Swarm intelligence where the knowledge of multiple individuals collectively creates an emergent pattern is seen in nature in abundance.

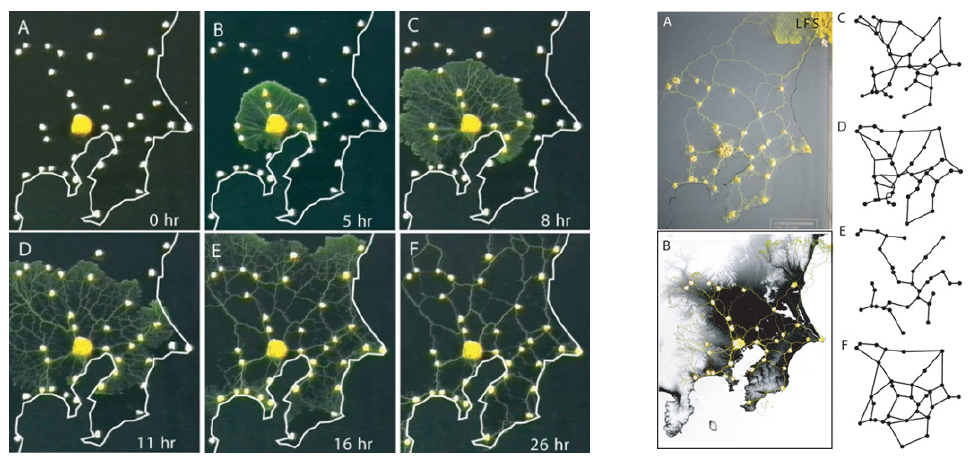
Tokyo rail network formation with Physarum polycephalum

Awad, Abubakr & Pang, Wei & Lusseau, David & Coghill, George. (2021).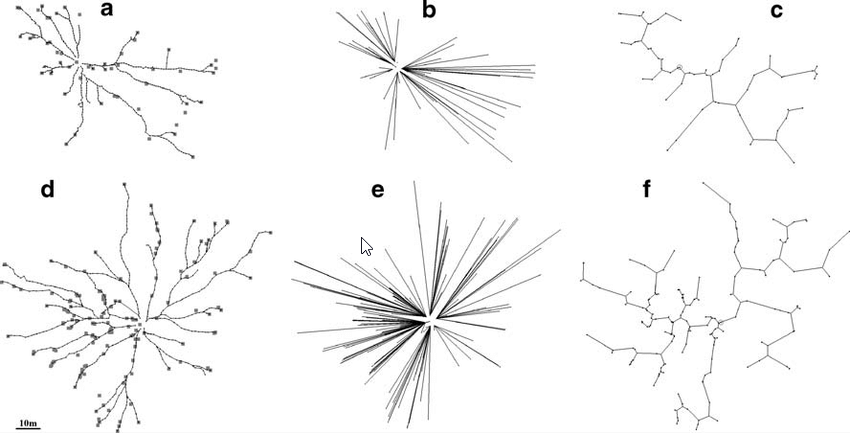

Shape and efficiency of wood ant foraging networks

Buhl, Jerome & Hicks, Kerri & Miller, Esther & Persey, Sophie & Alinvi, Ola & Sumpter, David. (2009).

These systems can also be modeled computationally to address connectivity challenges. In such landforms, designing an efficient road network is a complex task. However, by mimicking the collective intelligence found in nature, we can explore multiple approaches to develop a road network that aligns with the unique characteristics of the terrain. On our site, we can create analogs of these systems. By defining the metro stations as sources and the higher land as food, we can simulate collective intelligence to guide the design process.

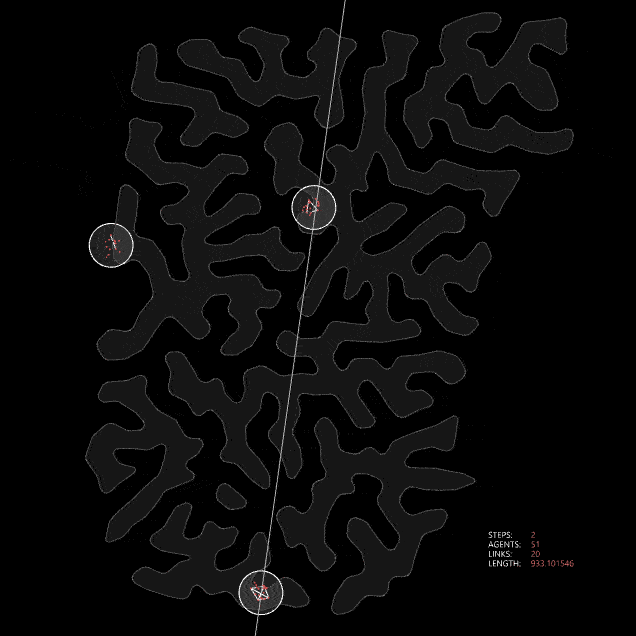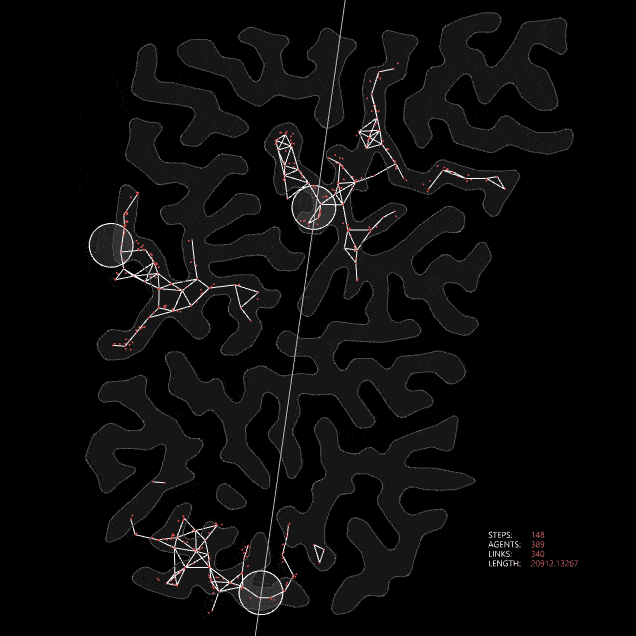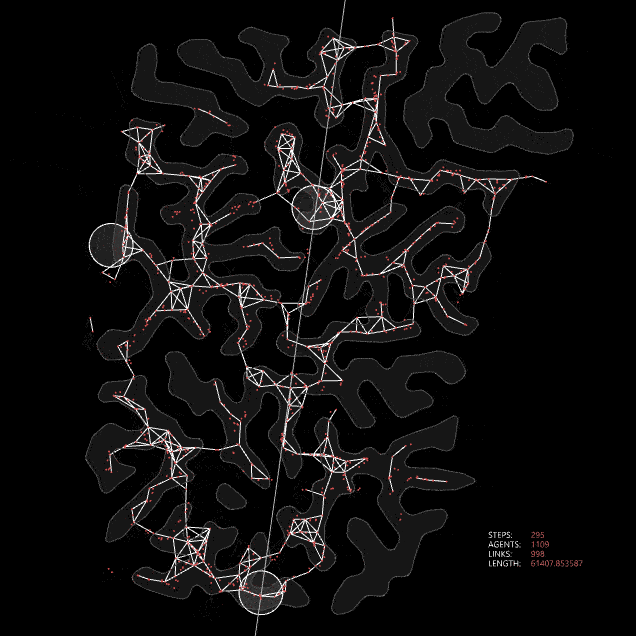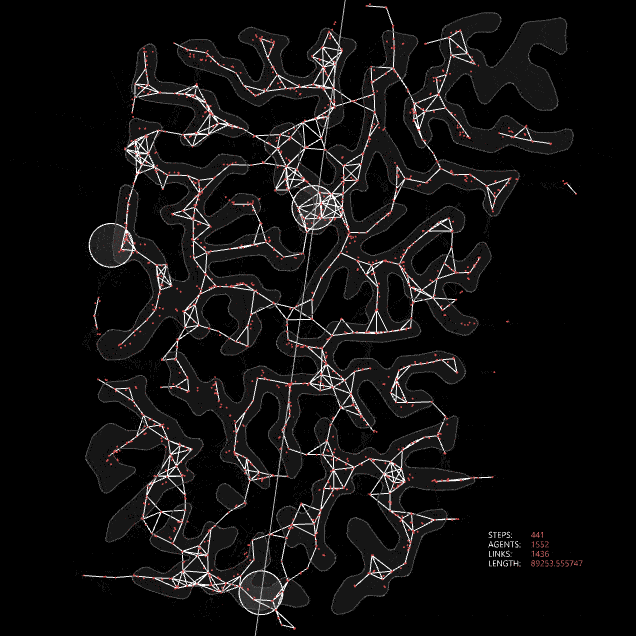
Slime mold algorithm applied to site

Zoning System

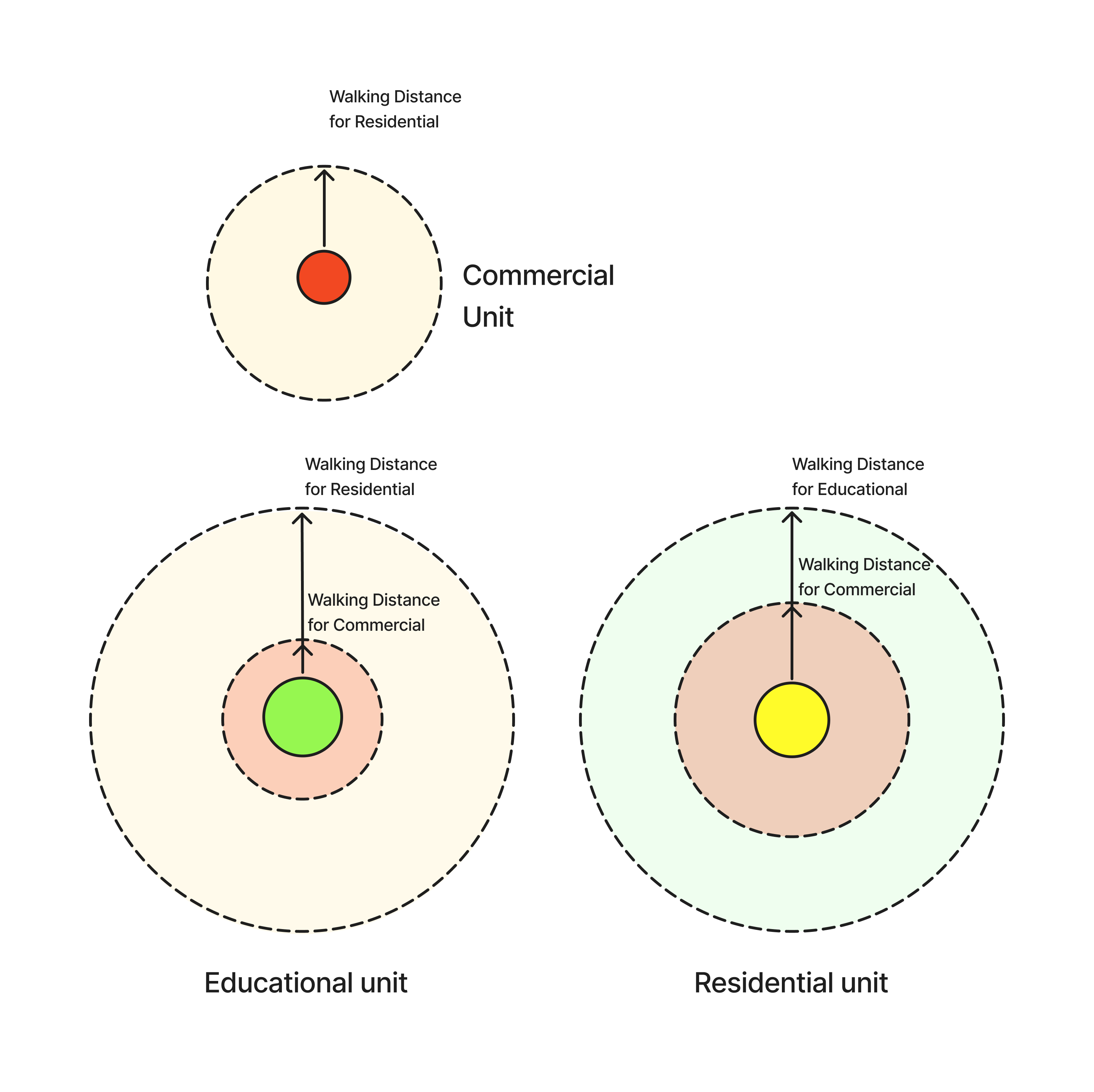
Natural settlements tend to grow organically in this type of landform. However, designing an efficient and walkable neighborhood in such areas is challenging. To address this, the natural settlement growth pattern can be simulated using walkability metrics.

Using walkability metrics, we can determine the optimal walking distances between different zones and calculate the demand for amenities based on the surrounding context. This natural growth process is driven by the relationship between demand and development. As a zone grows, it generates demand for additional amenities, creating a continuous cycle that shapes the settlement.

For example, in step one, the presence of residential units creates a demand for schools and shops nearby. In step two, new commercial and educational facilities emerge to meet this demand. However, this growth generates additional demand, which is addressed in step three, continuing the cycle.

python




__author__ = "prantoShohan"
__version__ = "2024.05.19"

import rhinoscriptsyntax as rs
import ghpythonlib.treehelpers as TH
import Grasshopper as gh
import Rhino.Geometry as R
import random as rand
import math

DistGraph = TH.tree_to_list(DISTANCES_GRAPH, retrieve_base=lambda y: y)
NbrhdGraph = TH.tree_to_list(NEIGHBOURHOOD_GRAPH, retrieve_base=lambda y: y)

DG = DistGraph

if "NG" not in globals() or RESET:
    NG = []
    for n in range(len(NbrhdGraph)):
        N = []
        for m in range(len(NbrhdGraph[n])):
            N.append(int(NbrhdGraph[n][m][1:]))
        NG.append(N)




MetroId = 302

InfluenceFactor = {
                #Demand per unit residential
                "Residential_Residential" : 1/150,
                "Residential_Educational" : 1/1500,
                "Residential_Healthcare" : 1/400,
                "Residential_SocioCultural" : 1/400,
                #Demand for commercial from different landuses
                "Residential_Commercial" : 1/50,
                "Commercial_Commercial" : -1,
                "Educational_Commercial" : 5,
                "Healthcare_Commercial" : 3,
                "SocioCultural_Commercial" : 2,
                #Self distance
                "Educational_Educational" : -1.5,
                "Healthcare_Healthcare" : -1.5,
                "SocioCultural_SocioCultural" : -1,
                #With metro
                "Metro_Residential" : 3,
                "Metro_Commercial" : 5,
                "Metro_Educational" : .5
                
            }

DistanceFactor = {
                #(B, d) d average walking distance(m)
                "Residential_Residential" : (1.71, 756),
                "Residential_Educational" : (2.01, 289),
                "Residential_Healthcare" : (1.71, 756),
                "Residential_SocioCultural" : (1.93, 289),
                
                "Residential_Commercial" : (2.14, 128),
                "Commercial_Commercial" : (2.14, 128),
                "Educational_Commercial" : (2.14, 128),
                "Healthcare_Commercial" : (2.14, 128),
                "SocioCultural_Commercial" : (2.14, 128),
                
                "Educational_Educational" : (2.01, 289),
                "Healthcare_Healthcare" : (1.71, 756),
                "SocioCultural_SocioCultural" : (2.14, 128),
                
                "Metro_Residential" : (1.71, 756),
                "Metro_Commercial" : (3, 756),
                "Metro_Educational" : (3, 128)
            }

class Block:
    def __init__(self, position, id):
        self.position = position
        self.id = int(id[1:])
        self.neighbours = [] 
        
        self.capacity = 20
        self.maxCapacity = 30
        
        self.demand = {
            "Residential" : 0.0,
            "Commercial" : 0.0,
            "Healthcare" : 0.0,
            "Educational" : 0.0,
            "SocioCultural" : 0.0
            }
        
        self.distribution = {
            "Residential" : 0.0,
            "Commercial" : 0.0,
            "Healthcare" : 0.0,
            "Educational" : 0.0,
            "SocioCultural" : 0.0, 
            "Metro" : 0.0
            }
        
        
       
    def addNeighbour(self, nbr, distance):
        self.neighbours.append((nbr, distance))
    
    def addNeighbours(self, nbrList, distanceList, blockList):
        assert(len(nbrList) == len(distanceList))
        for i in range(len(nbrList)):
            self.addNeighbour(blockList[nbrList[i] - 1], distanceList[i])
    
    def findNearest(self, type):
        distance = 500
        closestId = 301
        for nbr in self.neighbours:
            if(nbr[0].distribution[type] > 1):
                if (nbr[1] < distance):
                    closestId = nbr[0].id
                    distance = nbr[1]
        return((closestId, distance))
    
    def findNearestAll(self):
        print("Commercial: ", self.findNearest("Commercial")[1], " id: ", self.findNearest("Commercial")[0])
        print("Educational: ", self.findNearest("Educational")[1], " id: ", self.findNearest("Educational")[0])
        print("Healthcare: ", self.findNearest("Healthcare")[1], " id: ", self.findNearest("Healthcare")[0])
        print("SocioCultural: ", self.findNearest("SocioCultural")[1], " id: ", self.findNearest("SocioCultural")[0])
    
    def evaluateDemand(self):
        #print("##########Evaluating id:", self.id)
        
        for nbr in self.neighbours:
            if(nbr[1] != None):
                #print("Against id: ", nbr[0].id, " Distance: ", nbr[1])
                
                
                
                self.demand["Residential"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Residential"] * self.calculateDistanceFactor(nbr[1], "Residential_Residential")
                self.demand["Residential"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Residential"] * self.calculateDistanceFactor(nbr[1], "Metro_Residential") 
                self.demand["Residential"] = min(10, max(-10, self.demand["Residential"]))
                
                self.demand["Commercial"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Commercial"] * self.calculateDistanceFactor(nbr[1], "Metro_Commercial") 
                self.demand["Commercial"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Commercial"] * self.calculateDistanceFactor(nbr[1], "Residential_Commercial")
                self.demand["Commercial"] += nbr[0].distribution["Commercial"] * InfluenceFactor["Commercial_Commercial"] * self.calculateDistanceFactor(nbr[1], "Commercial_Commercial")
                self.demand["Commercial"] += nbr[0].distribution["Educational"] * InfluenceFactor["Educational_Commercial"] * self.calculateDistanceFactor(nbr[1], "Educational_Commercial")
                self.demand["Commercial"] += nbr[0].distribution["Healthcare"] * InfluenceFactor["Healthcare_Commercial"] * self.calculateDistanceFactor(nbr[1], "Healthcare_Commercial")
                self.demand["Commercial"] = min(10, max(-10, self.demand["Commercial"]))
                
                self.demand["Educational"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Educational"] * self.calculateDistanceFactor(nbr[1], "Metro_Educational")
                self.demand["Educational"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Educational"] * self.calculateDistanceFactor(nbr[1], "Residential_Educational")
                self.demand["Educational"] += nbr[0].distribution["Educational"] * InfluenceFactor["Educational_Educational"] * self.calculateDistanceFactor(nbr[1], "Educational_Educational")
                self.demand["Educational"] = min(10, max(-10, self.demand["Educational"]))
                
                self.demand["Healthcare"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Healthcare"] * self.calculateDistanceFactor(nbr[1], "Residential_Healthcare")
                self.demand["Healthcare"] += nbr[0].distribution["Healthcare"] * InfluenceFactor["Healthcare_Healthcare"] * self.calculateDistanceFactor(nbr[1], "Healthcare_Healthcare")
                self.demand["Healthcare"] = min(10, max(-10, self.demand["Healthcare"]))
                
                self.demand["SocioCultural"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_SocioCultural"] * self.calculateDistanceFactor(nbr[1], "Residential_SocioCultural")
                self.demand["SocioCultural"] += nbr[0].distribution["SocioCultural"] * InfluenceFactor["SocioCultural_SocioCultural"] * self.calculateDistanceFactor(nbr[1], "SocioCultural_SocioCultural")
                self.demand["SocioCultural"] = min(10, max(-10, self.demand["SocioCultural"]))
                
                
        occupiedSpace = self.distribution["Residential"] + self.distribution["Commercial"] * .5 + 5 * self.distribution["Educational"] + 5 * self.distribution["Healthcare"] + 3*self.distribution["SocioCultural"] 
        demandMultiplier = 1
        if (occupiedSpace > self.capacity):
            x = occupiedSpace - self.capacity
            demandMultiplier = -(x/self.capacity) + 1
        
#        demandMultiplier = min(1, max(-2, demandMultiplier))
        
        self.demand["Residential"] *= demandMultiplier
        self.demand["Commercial"] *= demandMultiplier
        self.demand["Educational"] *= demandMultiplier
        self.demand["Healthcare"] *= demandMultiplier
        self.demand["SocioCultural"] *= demandMultiplier

#        
#        self.demand["Residential"] = min(10, max(-10, self.demand["Residential"]))
#        self.demand["Commercial"] = min(10, max(-10, self.demand["Commercial"]))
#        self.demand["Educational"] = min(5, max(-5, self.demand["Educational"]))
        
    def evaluateDemandWithMetro(self):
#        print("##########Evaluating id:", self.id)
        
        for nbr in self.neighbours:
            if(nbr[1] != None):
#                print("Against id: ", nbr[0].id, " Distance: ", nbr[1])
#                print("Residential_Residential","distribution",nbr[0].distribution["Residential"],  "influence_factor:", InfluenceFactor["Residential_Residential"], "distance Factor:", self.calculateDistanceFactor(nbr[1], "Residential_Residential"))
                self.demand["Residential"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Residential"] * self.calculateDistanceFactor(nbr[1], "Residential_Residential")
                self.demand["Residential"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Residential"] * self.calculateDistanceFactor(nbr[1], "Metro_Residential") 
                
                self.demand["Commercial"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Commercial"] * self.calculateDistanceFactor(nbr[1], "Metro_Commercial") 
                self.demand["Commercial"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Commercial"] * self.calculateDistanceFactor(nbr[1], "Residential_Commercial") 
                self.demand["Commercial"] += nbr[0].distribution["Commercial"] * InfluenceFactor["Commercial_Commercial"] * self.calculateDistanceFactor(nbr[1], "Commercial_Commercial") 
                self.demand["Commercial"] += nbr[0].distribution["Educational"] * InfluenceFactor["Educational_Commercial"] * self.calculateDistanceFactor(nbr[1], "Educational_Commercial")
                
                self.demand["Educational"] += nbr[0].distribution["Metro"] * InfluenceFactor["Metro_Educational"] * self.calculateDistanceFactor(nbr[1], "Metro_Educational")
                self.demand["Educational"] += nbr[0].distribution["Residential"] * InfluenceFactor["Residential_Educational"] * self.calculateDistanceFactor(nbr[1], "Residential_Educational")
                self.demand["Educational"] += nbr[0].distribution["Educational"] * InfluenceFactor["Educational_Educational"] * self.calculateDistanceFactor(nbr[1], "Educational_Educational")
    

    def grow(self):
        self.distribution["Residential"] += int(self.demand["Residential"] * 1)
        self.distribution["Commercial"] += int(self.demand["Commercial"] * 1)
        self.distribution["Educational"] += int(self.demand["Educational"] * 1)
        self.distribution["Healthcare"] += int(self.demand["Healthcare"] * 1)
        self.distribution["SocioCultural"] += int(self.demand["SocioCultural"] * 1)
        
        self.distribution["Residential"] = max(0, self.distribution["Residential"])
        self.distribution["Commercial"] = max(0, self.distribution["Commercial"])
        self.distribution["Educational"] = max(0, self.distribution["Educational"])
        self.distribution["Healthcare"] = max(0, self.distribution["Healthcare"])
        self.distribution["SocioCultural"] = max(0, self.distribution["SocioCultural"])
        
        if (self.distribution["Educational"] >= 1):
            self.distribution["Commercial"] = 0
            self.distribution["Residential"] = 0
            self.distribution["Healthcare"] = 0
            self.distribution["SocioCultural"] = 0
        
        if (self.distribution["Healthcare"] >= 1):
            self.distribution["Commercial"] = 0
            self.distribution["Residential"] = 0
            self.distribution["Educational"] = 0
            self.distribution["SocioCultural"] = 0

    def calculateDistanceFactor(self, distance, relationship):
        #Distance influences P(d) = e^(-Bd)
        #https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3377942/
        distanceInfluence = math.e ** ( - DistanceFactor[relationship][0] * distance/1609.34 ) # meter to miles
        return distanceInfluence 
    
    def __str__(self):
        s = " ID: "+str(self.id) + ", Neighbours: "
        for n in self.neighbours:
            s += " id: "+str(n[0].id) +  "- distance: "+str(n[1])
        return s


################## ID = index+1  #################

def initial_influence():
    for b in range(len(Blocks)):
        Blocks[b].evaluateDemandWithMetro()

def demand_loop():
    for b in range(len(Blocks)):
        Blocks[b].evaluateDemand()
def grow_loop():
    for b in range(len(Blocks)):
        Blocks[b].grow()

def main():

    demand_loop()
    grow_loop()





# Instantiate or reset persistent counter variable
if "c" not in globals() or RESET:
    c = 0

if "Blocks" not in globals() or RESET:
    Blocks = []
    for n in range(len(BLOCKS)):
        Blocks.append(Block(BLOCKS[n], BLOCKS_ID[n]))
    for b in range(len(Blocks)):
        Blocks[b].addNeighbours(NG[b], DG[b], Blocks)
        
    Blocks[MetroId-1].distribution["Metro"] = 1
    Blocks[246].distribution["Metro"] = 1
    initial_influence()


# Update the variable and component
if (c < ITERATIONS):
    c = c + 1
    main()

COUNTER = c


Points = []
Ids = []
RD = []
CD = []
ED = []
HD = []
SD = []

RDist = []
CDist = []
EDist = []
HDist = []
SDist = []

for p in Blocks:
    Points.append(p.position)
    Ids.append(p.id)
    RD.append(p.demand["Residential"])
    CD.append(p.demand["Commercial"])
    ED.append(p.demand["Educational"])
    HD.append(p.demand["Healthcare"])
    SD.append(p.demand["SocioCultural"])
    
    RDist.append(p.distribution["Residential"])
    CDist.append(p.distribution["Commercial"])
    EDist.append(p.distribution["Educational"])
    HDist.append(p.distribution["Healthcare"])
    SDist.append(p.distribution["SocioCultural"])

points = Points
ids = Ids

RESIDENTIAL_DEMAND = RD
COMMERCIAL_DEMAND = CD
EDUCATIONAL_DEMAND = ED
HEALTHCARE_DEMAND = HD
SOCIOCULTURAL_DEMAND = SD

RESIDENTIAL_DISTRIBUTION = RDist
COMMERCIAL_DISTRIBUTION = CDist
EDUCATIONAL_DISTRIBUTION = EDist
HEALTHCARE_DISTRIBUTION = HDist
SOCIOCULTURAL_DISTRIBUTION = SDist

Blocks[287].findNearestAll()
    
#Blocks = []
#
#for b in range(len(BLOCKS)):
#    Blocks.append(Block(BLOCKS[b], BLOCKS_ID[b]))
#
#def findBlock(blocks, id):
#    for b in blocks:
#        if b.id == id:
#            return b
#        else:
#            print ("not found")
#
#for n in range(len(Blocks)):
#    for m in range(len(NbrhdGraph[n])):
#        Blocks[n].addNeighbour(findBlock(Blocks, int(NbrhdGraph[n][m][1:])), DistGraph[n][m])
#
#
#print(Blocks[1])

The demand is calculated using this formula: the demand for any amenity depends on three factors—the number of requesters for that amenity, the required number of amenities per requester unit, and the walkability distance factor.

The algorithm is tested on a small network, following the cycle of calculating demand and adding the required zones. Over time, the cycle stabilizes, reaching equilibrium after approximately 50 steps. At this point, the required amenities are positioned to serve the maximum number of people within a walkable distance.

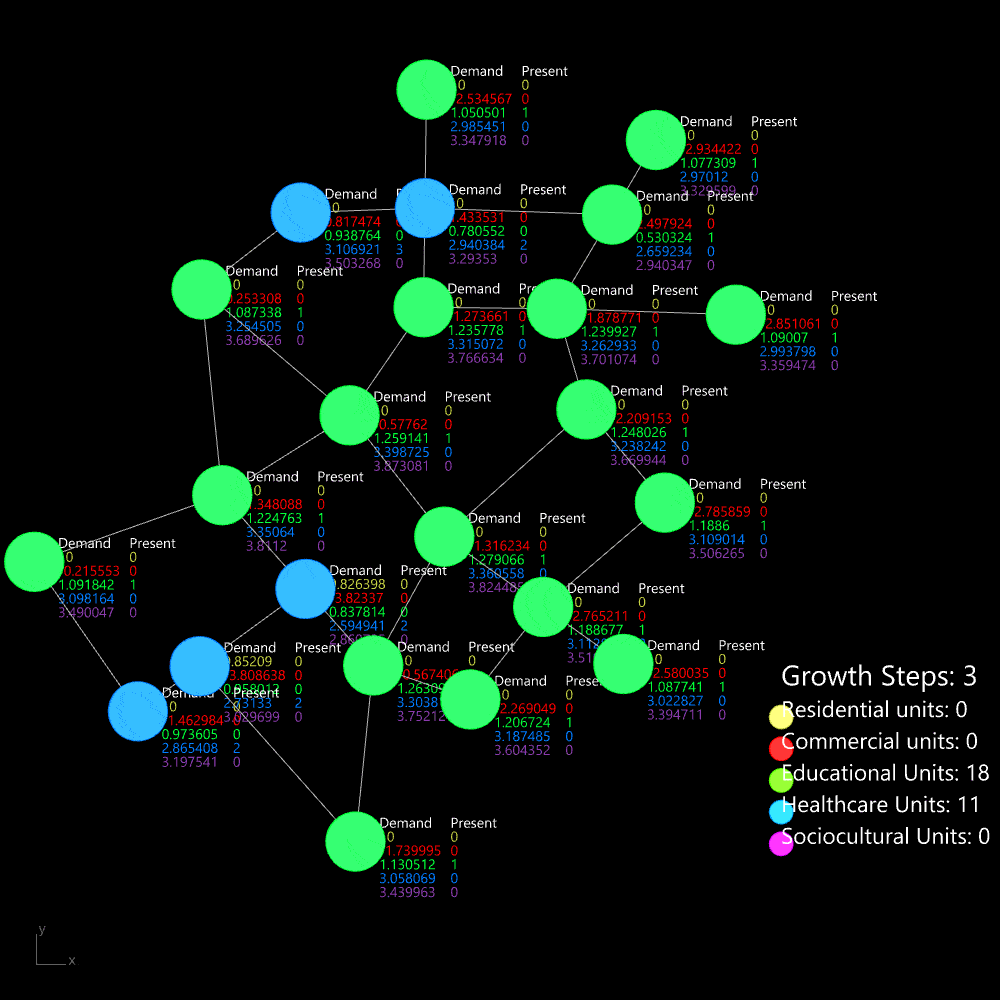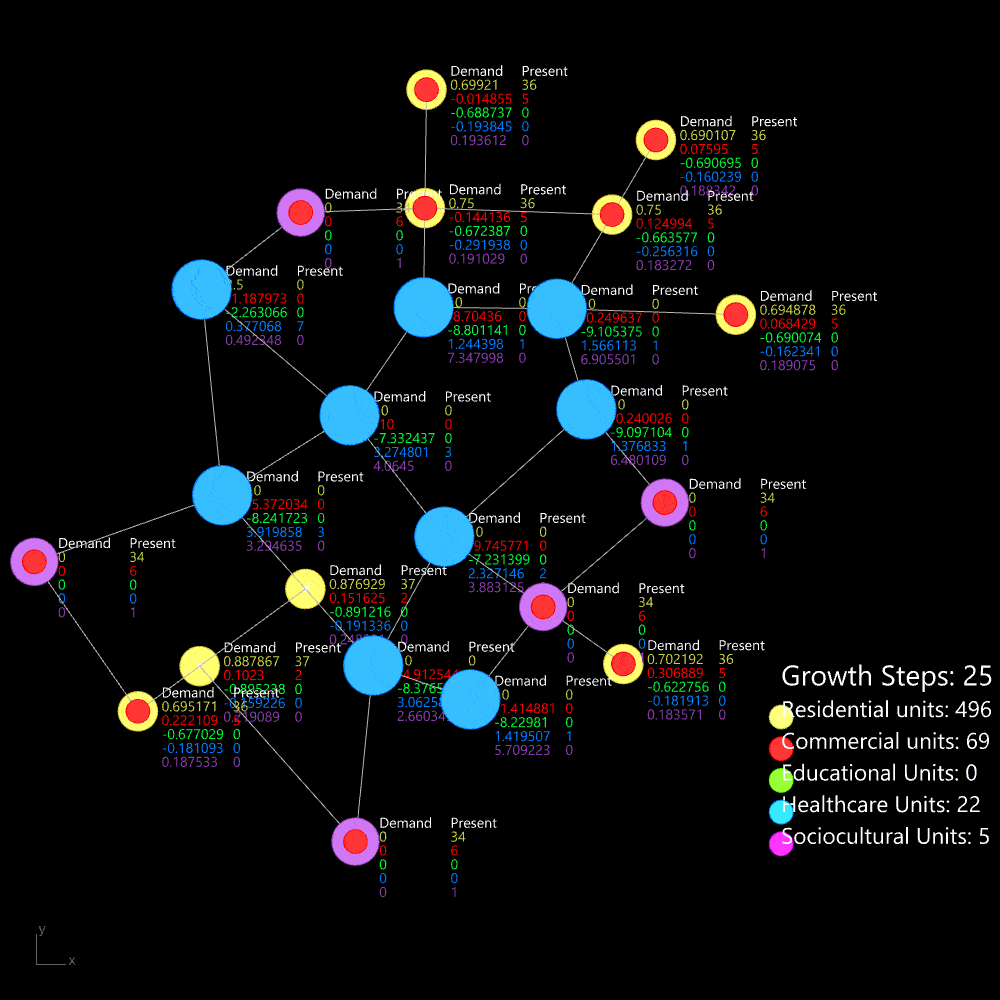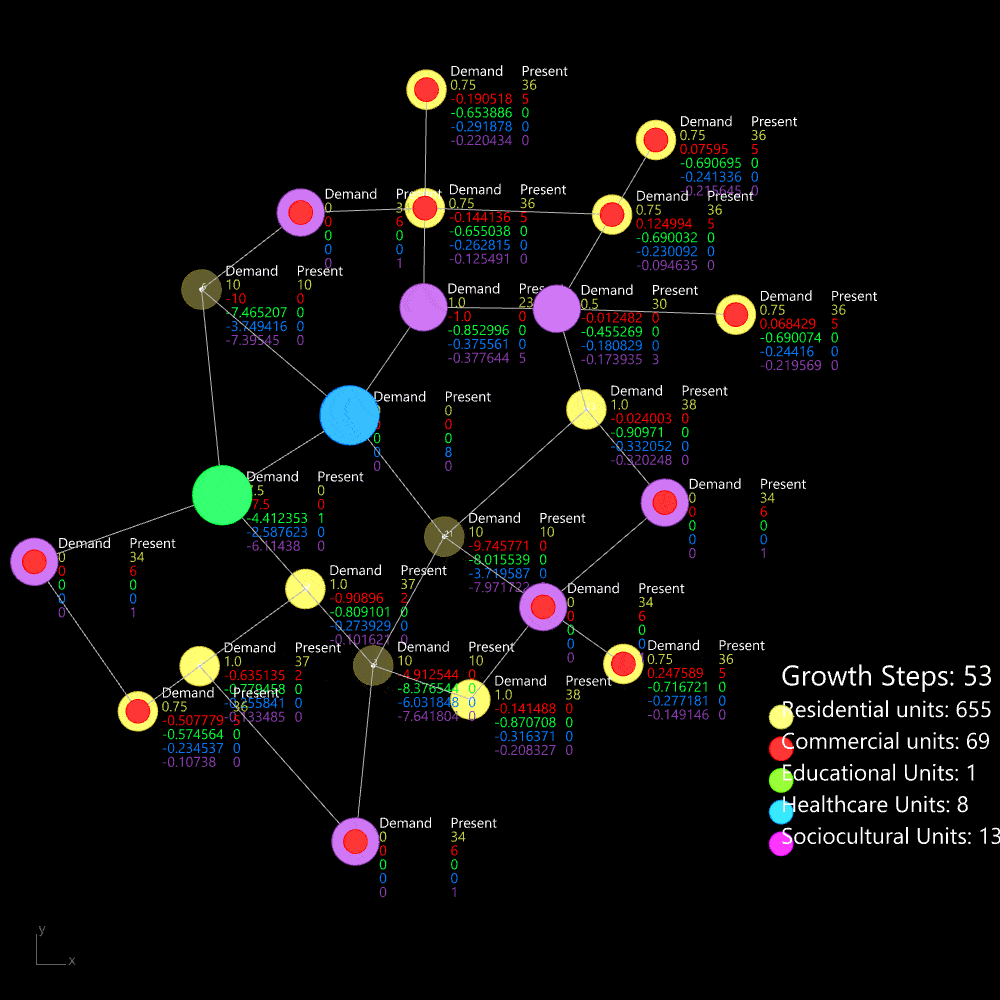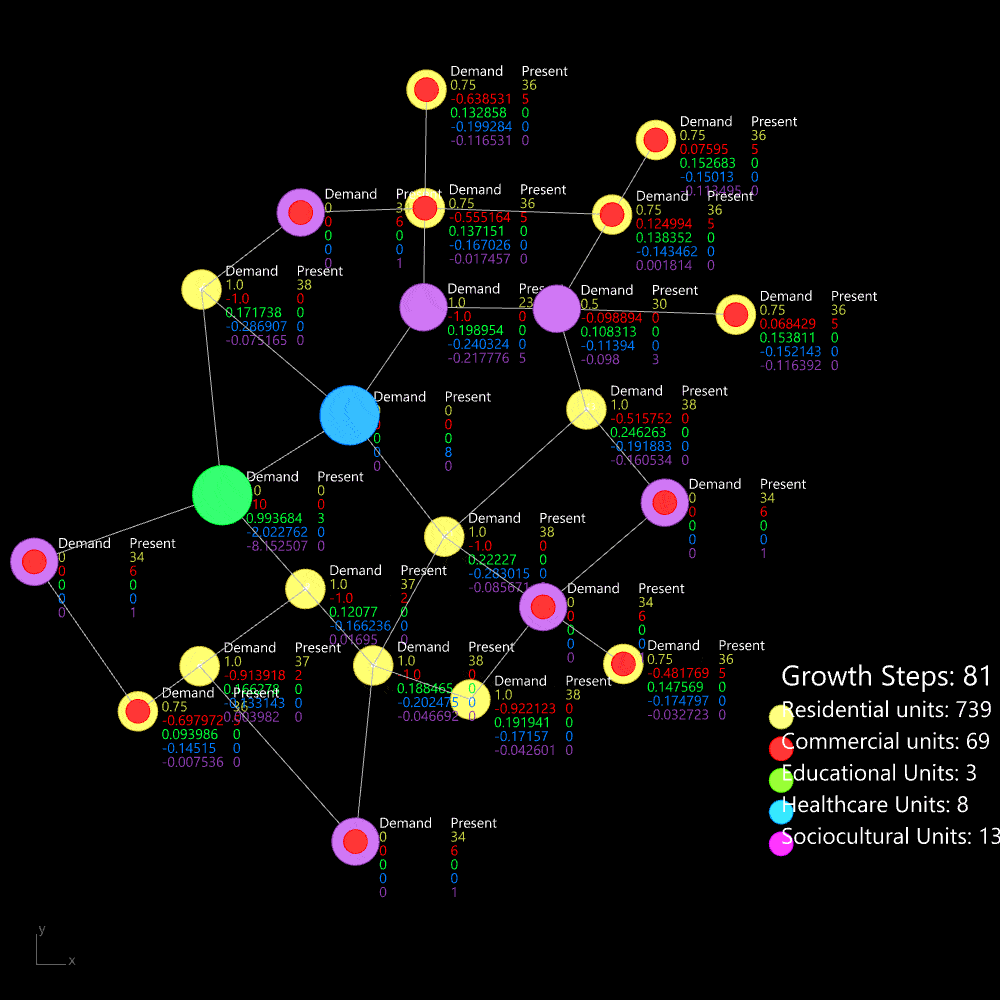
Organic growth algorithm applied on a simple network

Then it is applied to our site which has a much larger area and more complex network. It also reaches an equilibrium in around step 35.

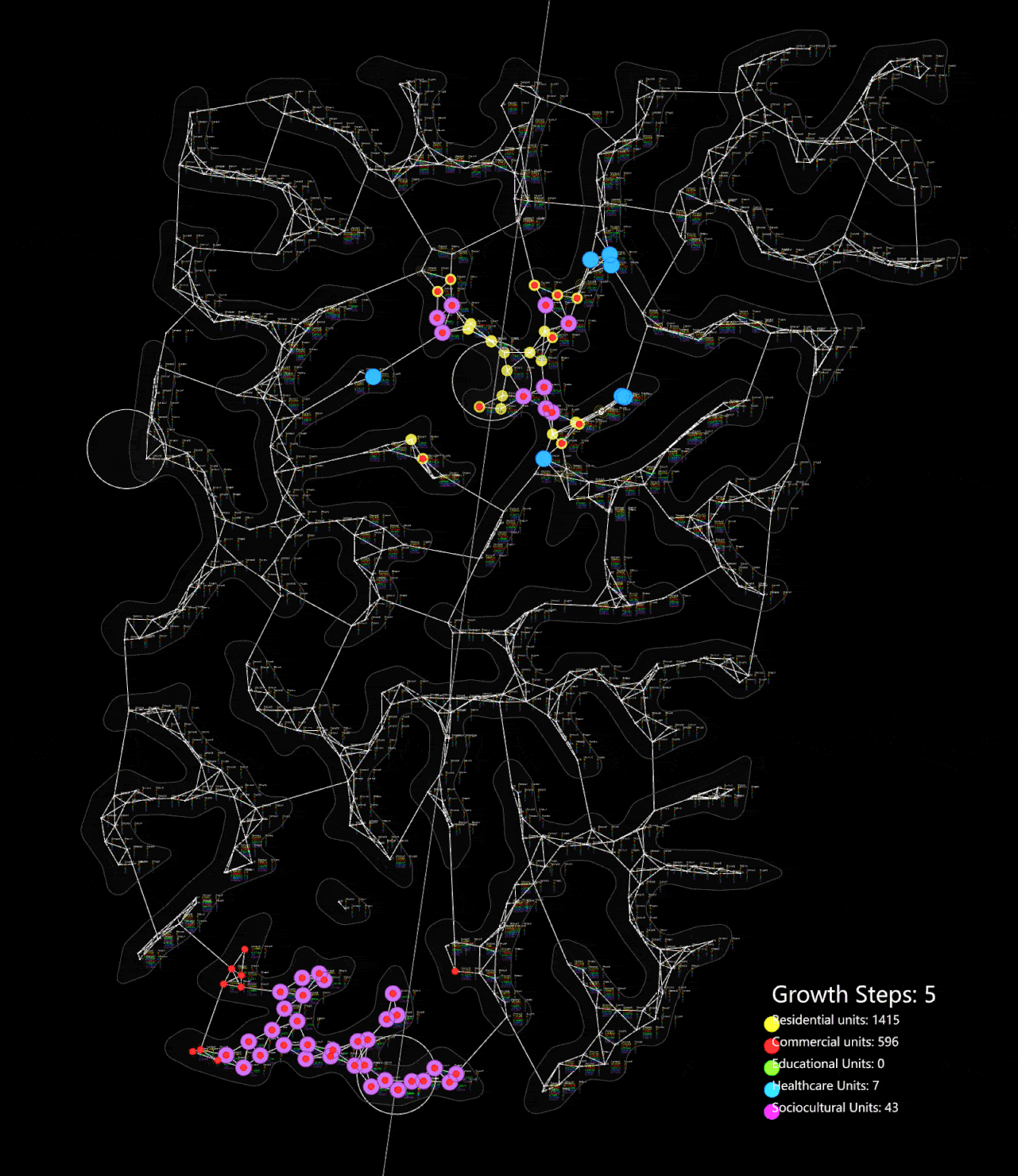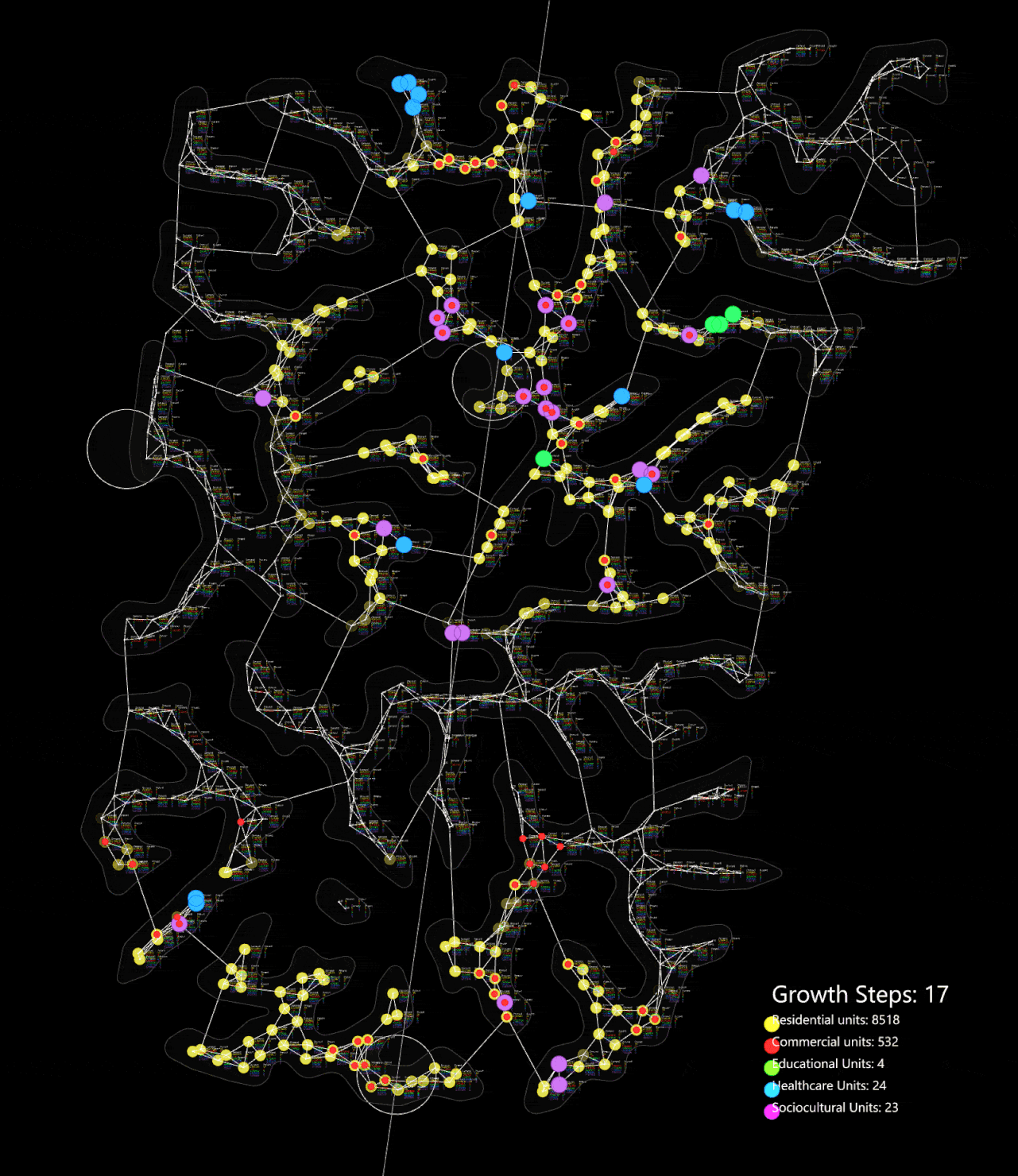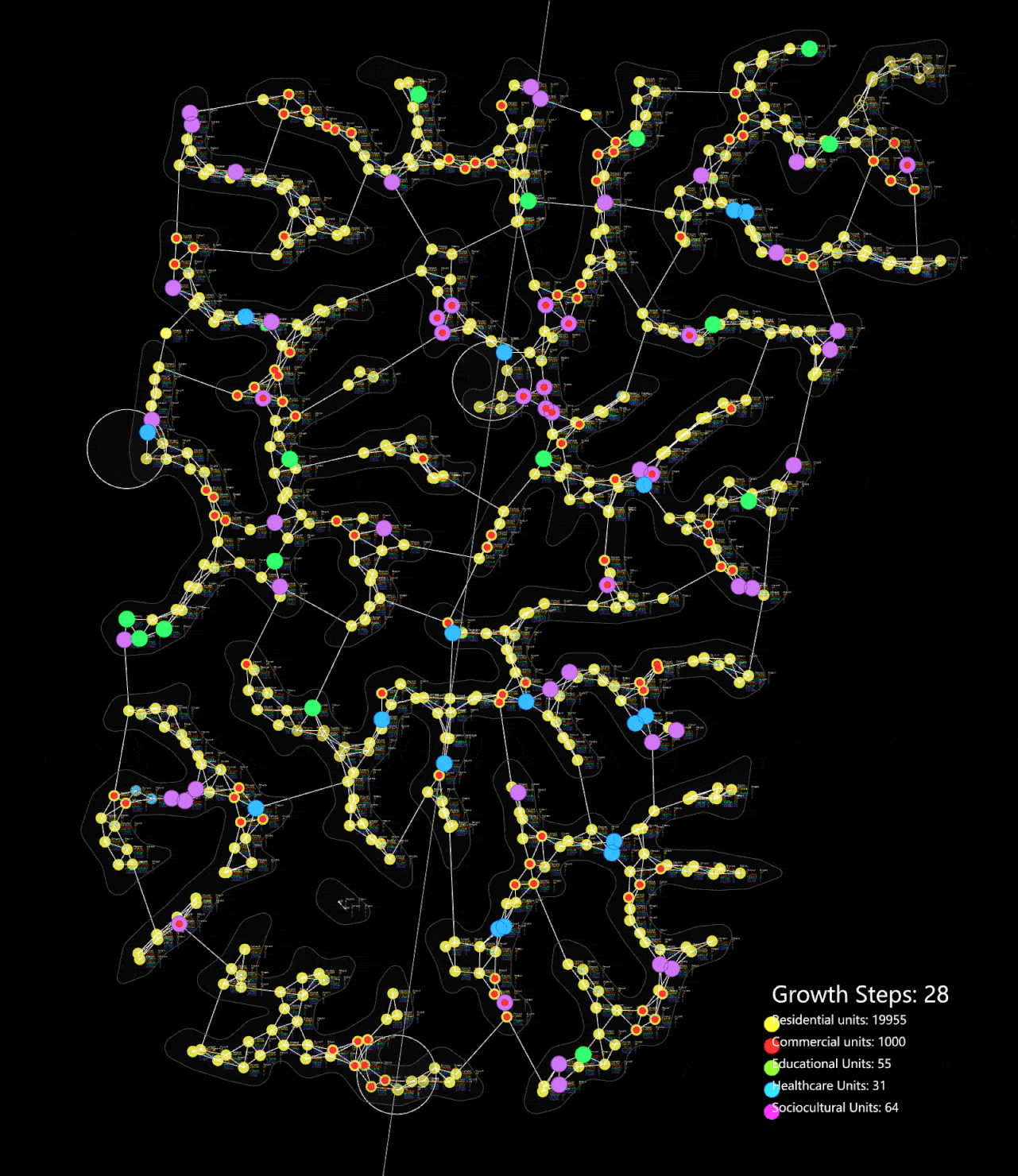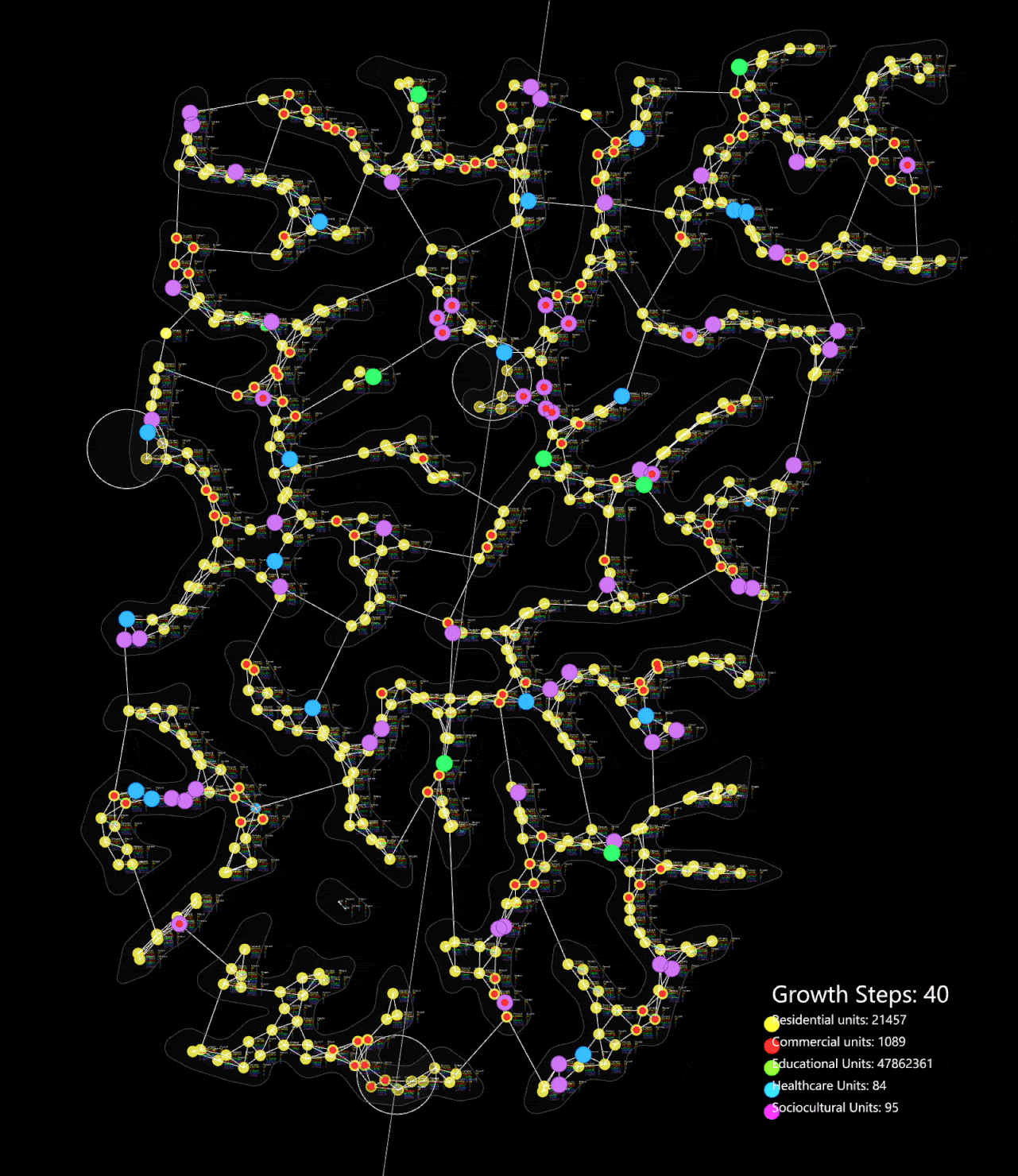
Organic growth algorithm applied on the network

Efficiency of Urban Organism

Effecient systems designed through collective intelligence.

This is a kind of swarm intelligent or cellular automata, where each agent reacts with its neighbours. The cycle of growth and demand is a dynamical system. After the system reaches an equilibrium, a solution is found.

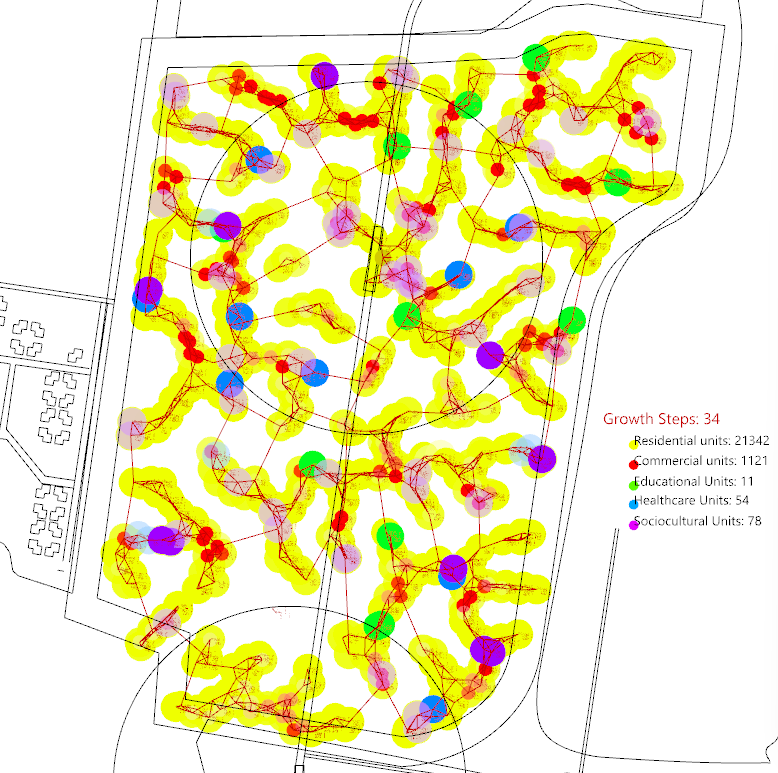
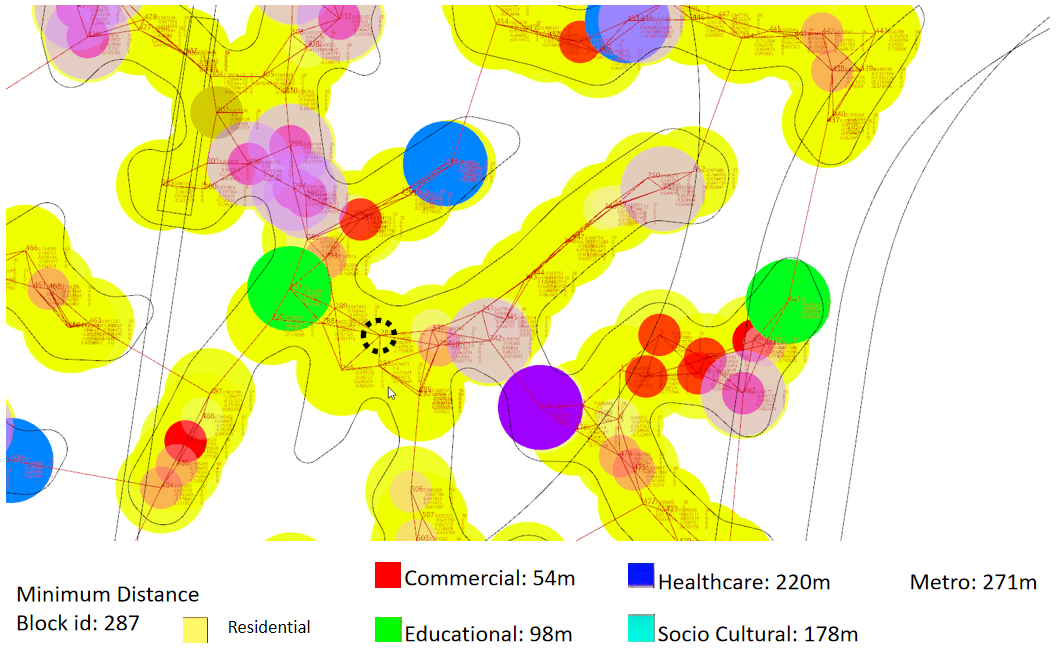
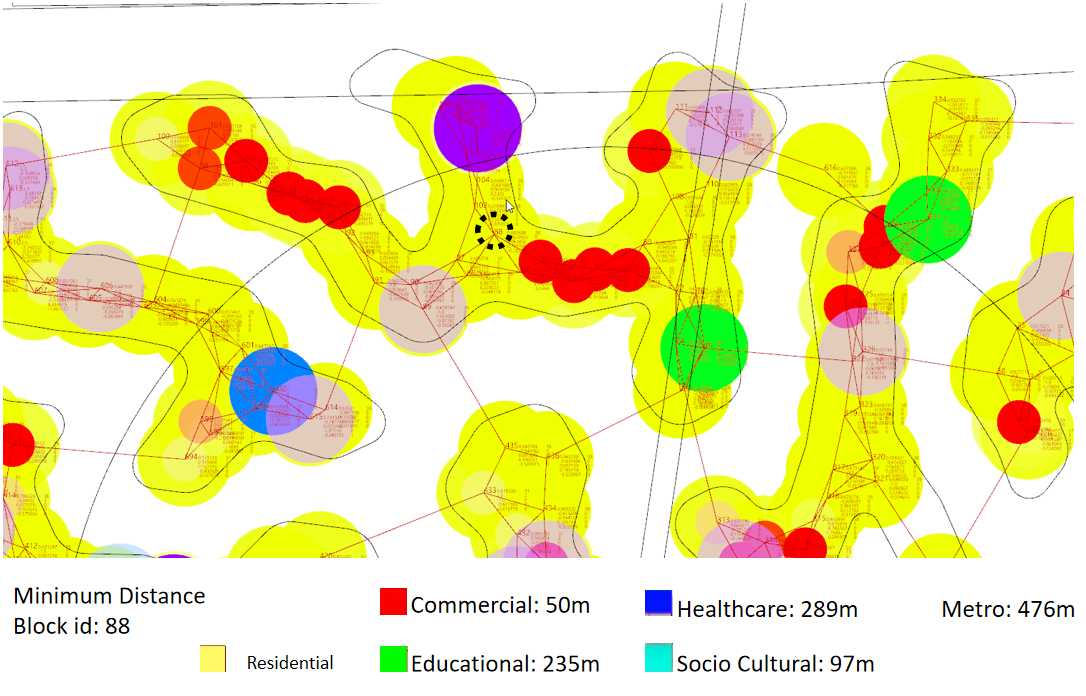
In these two examples, the distance from different amenities are shown. All amenities are within walking distance.

Landscape and Walkability

The land water interface supports the most important ecosystems.

The ecosystem of the edge plays a vital role in these landscapes. Along the long edge, vegetable gardens, wild plants, and ponds create a rich and diverse environment. The roads are designed to encourage walking and cycling, with public trails running along the edge to enhance accessibility and connection to nature.

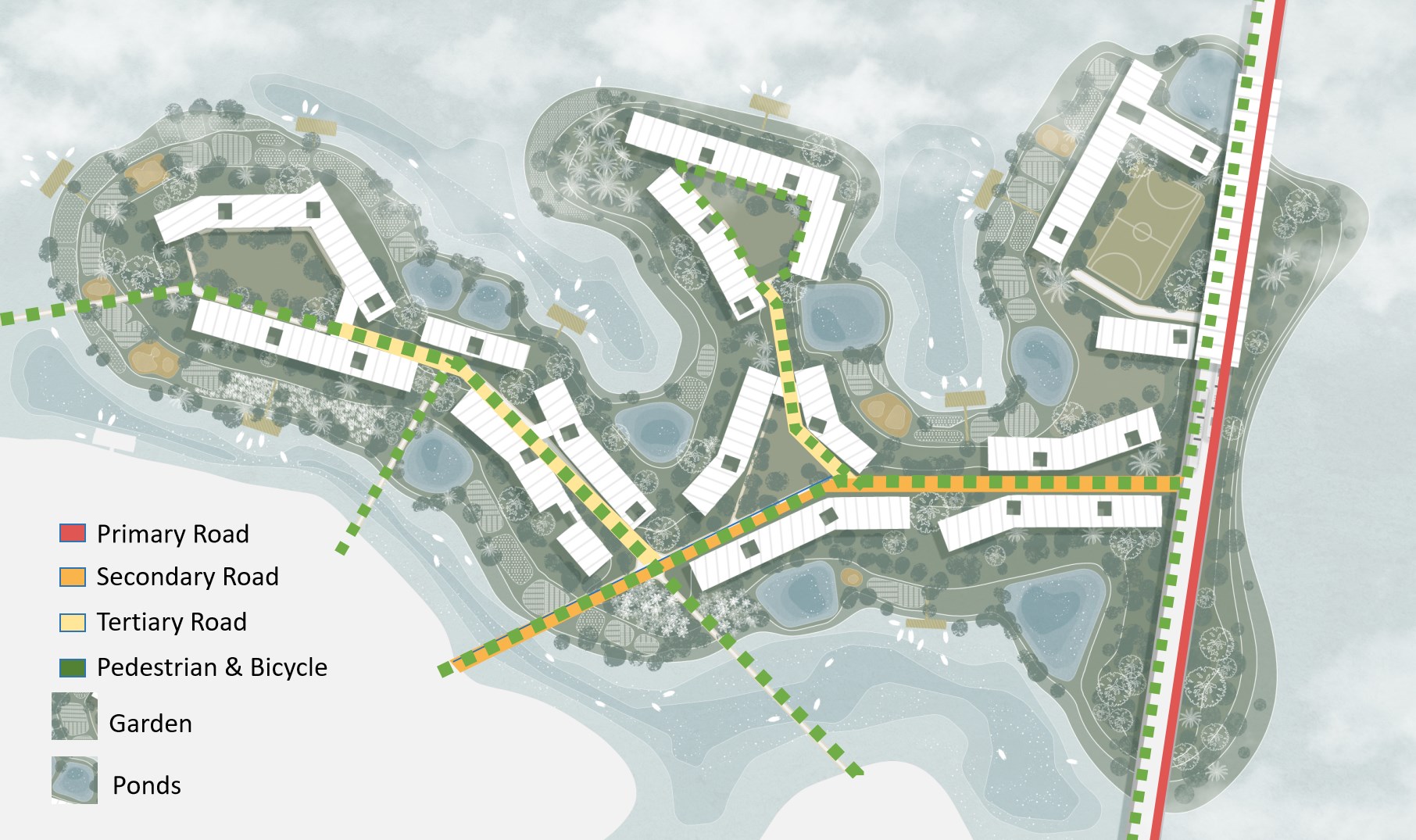
The extensive network of water channels allows for connectivity across the region, as all water bodies are interlinked. This makes water-based transportation a viable option, a method that was historically prevalent in Dhaka.

This project explores how computational modeling can mimic organic systems to design more efficient and sustainable urban environments. By simulating natural processes like resource cycles and growth patterns, we can optimize city planning for better connectivity, walkability, and ecosystem integration. The use of water-based transportation and edge ecosystems, inspired by Dhaka’s unique landscape, demonstrates how cities can grow intelligently, much like organisms, through a dynamic, demand-driven approach.

Pranto Shohan 2024